多項式的微積分

先備練習

1. 將 (1+1) 從一次方乘到四次
2. 將 (x+1) 從一次方乘到四次
3. 將 (a+b) 從一次方乘到四次

• 多項式
  1. 項
  2. 係數
  3. 次
  4. 元
• 楊輝三角形：${(a+b)}^n$ 展开的系数

切線斜率、微分、導數

設 $y=f(x)$，則函數 $f$在 $a$點切線斜率、微分、導數、$f^{\prime }(a)$、$\frac{dy}{dx}$、$\frac{df(x)}{dx}$、$\frac{\mathrm{\Delta }f(x)}{\mathrm{\Delta }x}$、$\underset{\mathrm{\Delta }x\to 0}{\lim }\frac{f(a+\mathrm{\Delta }x)-f(a)}{\mathrm{\Delta }x}$ 都代表同一個意思。

一元多次方程式的微分

微分的方法

y=ƒ(x)：

• 單項式的 ƒ'(x)

  $f(x)=a{x}^n$

  $f^{\prime }(x)=an{x}^{n-1}$

  1. axⁿ 對 x 的微分為 anx^n-1 ，請證明
  2. n 為 0 (即常數)，則微分為 0。因為微分代表「變化」，常數沒有變化。
  3. 除 0 之外，n 不管是正數或負數、整數或非整數都成立，
• 多項式的 ƒ'(x)
  1. 每個單項皆微分
  2. 常數項微分為 0
• 微分之應用問題
• 更多例題

與微分的相關的性質

• 極限存在，它的左右極限存在且相等。
• 函數在一點可導的條件是：函數在該點的左右兩側導數都存在且相等。
• dy=ƒ'(x) dx 即 ƒ'(x) 曲線與 $x$ 軸所夾的微小面積。

長條面積總和

函數 y = x² 的上長條總和

函數 y = x² 的下長條總和

• 原函數 ƒ(x)=0 時，x 值稱為方程式的根。此處為函數圖形與 $x$ 軸之交點。
• 函數 ƒ(x) 與其導數函數 ƒ'(x) 的關係：
  1. 函數的轉彎處 → 斜率為 0，ƒ'(x) 為 0 處，ƒ(x) 有極大值或極小值，斜率由正轉負時有極大值，斜率由負轉正時有極小值。
  2. 一系列的函數 ƒ(x) + C ，有相同的導函數 ƒ'(x) 。

求導法則

適用所有可微分的方程式。

法則	表示式	簡記	口訣
常數微分	$\frac{dC}{dx}=0$	常數'=0	常數微分為零
常係數微分	$\frac{d(C\times f(x))}{dx}=C\times \frac{d(f(x))}{dx}$	(Cƒ(x))'=Cƒ'(x)	常係數可提出
乘積法則	$\begin{array}{cc}\frac{d(f(x)\times g(x))}{dx}& =\frac{d(f(x))}{dx}\times g(x)+f(x)\times \frac{d(g(x))}{dx}\\ & =f^{\prime }(x)\times g(x)+f(x)\times g^{\prime }(x)\end{array}$	(fg)'=f'g+fg'	前導後不導 +前不導後導
鏈式法則	$\frac{d(f(x))}{dx}=\frac{d(f(x))}{d(g(x))}\times \frac{d(g(x))}{dx}$ 或 $d(f(x))=d(f(x))\times \frac{d(g(x))}{d(g(x))}$	$\frac{dy}{dx}=\frac{dy}{dz}\cdot \frac{dz}{dx}$	分子分母同乘d(g(x))

多項式的圖形

1. 零次：，
2. 一次：，
3. 二次：，，更多拋物線圖形
4. 三次：，
5. 四次：，
6. 五次：，

一元二次方程式的配方法

由乘法公式 $(m+n{)}^2=m^2+2mn+n^2$，可以對任意一元二次方程式 $a{x}^2+bx+c=0$ 進行配方，而以上的公式解也是由配方法推導出來的，推導過程如下：

推導過程一：求函數值

$\begin{array}{cc}y& =f(x)\\ \\ & =a{x}^2+bx+c\\ \\ & =a(x^2+\frac{b}{a}x+\frac{c}{a})\\ \\ & =a[x^2+2\left(\frac{b}{2a}\right)x+\frac{c}{a}]\\ \\ & =a[x^2+2\left(\frac{b}{2a}\right)x+{\left(\frac{b}{2a}\right)}^2-{\left(\frac{b}{2a}\right)}^2+\frac{c}{a}]\\ \\ & =a[{(x+\frac{b}{2a})}^2-{\left(\frac{b}{2a}\right)}^2+\frac{4ac}{4a^2}]\\ \\ & =a[{(x+\frac{b}{2a})}^2+\frac{4ac-b^2}{4a^2}]\\ \\ & =a{(x+\frac{b}{2a})}^2+(c-\frac{b^2}{4a})\\ \end{array}$

函數值與圖形的關係

1. $a>0$ 時右側斜向上，拋物線開口向上，有極小值
2. $a<0$ 時右側斜向下，拋物線開口向下，有極大值
3. $x+\frac{b}{2a}=0$ 或 $x=-\frac{b}{2a}$ 時有極大值或極小值 $c-\frac{b^2}{4a}$
4. $a{(x+\frac{b}{2a})}^2+(c-\frac{b^2}{4a})=0$（即圖形交 $y=0$）時為兩根

推導過程二：求根

$a{x}^2+bx+c=0⟹x^2+\frac{b}{a}x+\frac{c}{a}=0$

$x^2+\frac{b}{a}x+\frac{c}{a}=0⟹x^2+2\left(\frac{b}{2a}\right)x+\frac{c}{a}=0$

$x^2+2\left(\frac{b}{2a}\right)x+\frac{c}{a}=0⟹x^2+2\left(\frac{b}{2a}\right)x+{\left(\frac{b}{2a}\right)}^2+\frac{c}{a}={\left(\frac{b}{2a}\right)}^2$

$x^2+2\left(\frac{b}{2a}\right)x+{\left(\frac{b}{2a}\right)}^2+\frac{c}{a}={\left(\frac{b}{2a}\right)}^2⟹x^2+2\left(\frac{b}{2a}\right)x+{\left(\frac{b}{2a}\right)}^2={\left(\frac{b}{2a}\right)}^2-\frac{c}{a}$

$x^2+2\left(\frac{b}{2a}\right)x+{\left(\frac{b}{2a}\right)}^2={\left(\frac{b}{2a}\right)}^2-\frac{c}{a}⟹{(x+\frac{b}{2a})}^2=\frac{b^2-4ac}{4a^2}$

${(x+\frac{b}{2a})}^2=\frac{b^2-4ac}{4a^2}⟹x+\frac{b}{2a}=\pm \frac{\sqrt{b^2-4ac}}{2a}$

$x+\frac{b}{2a}=\pm \frac{\sqrt{b^2-4ac}}{2a}⟹x=\frac{-b\pm \sqrt{b^2-4ac}}{2a}$

根與係數的關係

設一元二次方程式 $a{x}^2+bx+c=0$ 的解為 $w$ 和 $z$ ，則有以下關係式：

• $w+z=-\frac{b}{a}$

• $wz=\frac{c}{a}$

這兩個公式由設 $w$ 和 $z$ 為符合一元二次方程式公式解的寫法來求出。

基本例題

1. $x^2=16$
2. $x^2-x=30$
3. $4x^2+4x+4=3$

配方法的圖解

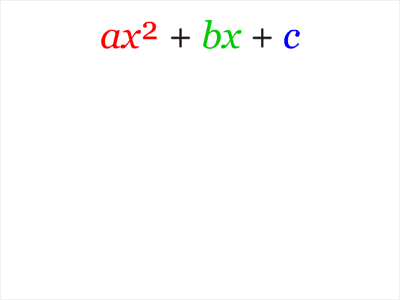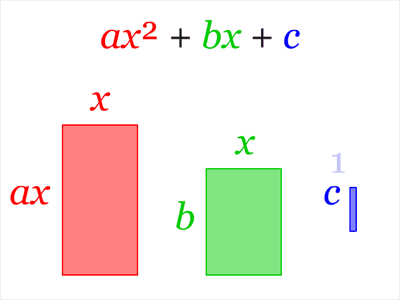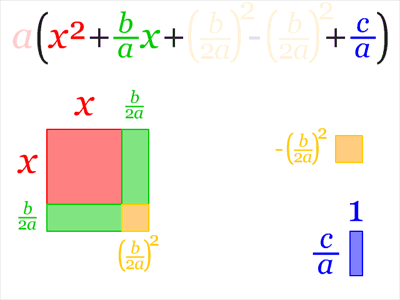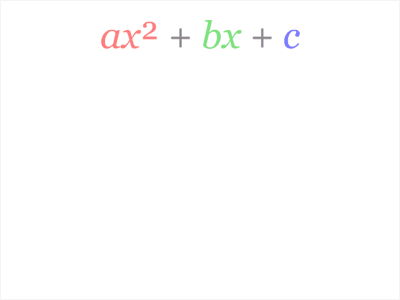File:Completing the square.ogv	令 a=1,C=-c