三角形的五心

定義

三角形五心的定義

三角形的內心、外心、重心及垂心稱為三角形的四心，定義如下：

名稱	定義	圖示	備註
內心	三個內角的角平分線的交點		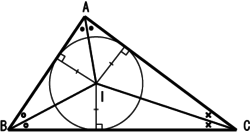該點為三角形內切圓的圓心。
外心	三條邊的垂直平分線的交點		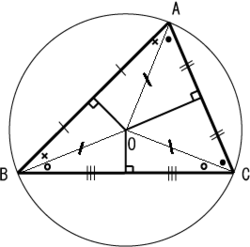該點為三角形外接圓的圓心。
重心	三條中線的交點		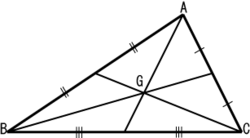被交點劃分的線段比例為1:2(靠近角的一段較長)。
垂心	三條高線的交點

垂心(藍)、重心(黃)和外心(綠)能連成一線，且成比例2:1，稱為尤拉線。

連同以下的旁心，合稱為三角形的五心：

名稱	定義	圖示	備註
旁心	其中一內角和另外兩外角的角平分線的交點		有三個，為三角形某一邊上的旁切圓的圓心。

正弦(sine)、餘弦(Cosine)定義

∠A之度數為α：
sinα=對邊長/斜邊長
cosα=鄰邊長/斜邊長

直角三角形中∠A之度數為α，定義：

sinα=對邊長/斜邊長

cosα=鄰邊長/斜邊長

基本性質：

1. sinα=cos(90°-α)

   令∠B度數為β，β=90°-α，則sinα=a/c=cosβ=cos(90°-α)

2. cosα=sin(90°-α)

   令∠B度數為β，β=90°-α，則cosα=b/c=sinβ=sin(90°-α)

3. sin²α+cos²α=1

三角函數的平方寫在角度前，不寫在角度後，以和「α²取sin」區分。

${\sin }^2\alpha +{\cos }^2\alpha =\frac{a^2}{c^2}+\frac{b^2}{c^2}=\frac{c^2}{c^2}=1$

兩大公式

(一)圓周角等於對同弧圓心角的一半

正弦定理

若$R$為外接圓半徑，則 $\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R$。

(二)餘弦定理

$c^2=a^2+b^2-2ab\cos \gamma$

$b^2=c^2+a^2-2ca\cos \beta$

$a^2=b^2+c^2-2bc\cos \alpha$

三角形面積公式

(一)已知兩邊及其夾角

三角形面積為二分之一兩邊乘以夾角正弦。

△=$\frac{1}{2}\times ab\times \sin \gamma$

△=$\frac{1}{2}\times b\times h=\frac{1}{2}\times b\times h\times \frac{a}{a}=\frac{1}{2}\times a\times b\times \frac{h}{a}=\frac{1}{2}\times ab\times \sin \gamma$

(二)海倫公式

$s=\frac{a+b+c}{2}$

△=$\sqrt{s(s-a)(s-b)(s-c)}$

(三)內切圓半徑

$s=\frac{a+b+c}{2}$，r為內切圓半徑

△面積 $=sr$

(四)外接圓半徑

R為外接圓半徑

△=$\frac{abc}{4R}$

證明

(六)三高

△= ½×a×h_a= ½×b×h_b= ½×c×h_c

(七)以三點座標求面積

△=$\pm \frac{1}{2}\left|\begin{array}{cc}{x}_2-x_1& y_2-y_1\\ x_3-x_1& y_3-y_1\end{array}\right|$

如 (x₁,y₁) 為 (0,0) 即原點，則

△=$\pm \frac{1}{2}\left|\begin{array}{cc}{x}_2& y_2\\ x_3& y_3\end{array}\right|$

再旋轉使 (x₃,y₃) 位於 X 軸，為 (x₃,0)。此時 x₃ 為底， y₂ 為高：

△=$\frac{1}{2}\left|\begin{array}{cc}{x}_2& y_2\\ x_3& 0\end{array}\right|=-\frac{1}{2}{x}_3{y}_2$

從一角出發，其兩邊的向量為 $𝐚$ 及 $𝐛$

△=$\frac{1}{2}|𝐚\times 𝐛|$